Integral de sen^5(x) dx – Método numérico

No post passado abordamos a resolução desta integral, a integral de sen^5(x) dx, que à primeira vista parece simples (e de fato é…), mas existem outras maneiras de resolver uma integral definida, especialmente quando lidamos com casos de difícil ou até mesmo impossível integração, ou quando tratamos de um conjunto de dados sem um modelo matemático simples. E

Entretanto, esses métodos, conhecidos como métodos numéricos, incluem o Trapézio, 1/3 de Simpson e 3/8 de Simpson. Portanto, hoje, concentraremos nossa atenção na Regra do Trapézio.

Todavia, não se preocupe, pois exploraremos todos os detalhes dessa técnica.

De maneira geral, o processo de resolução utilizando esses métodos baseia-se em dividir o intervalo em partes iguais, encontrar valores igualmente espaçados dentro dessas partes, multiplicá-los por um “vetor” característico que depende do método escolhido e, em seguida, realizar operações simples de somatório e multiplicação. Abordaremos esses detalhes em breve. Por enquanto, vamos nos aprofundar um pouco mais na parte teórica.

Integral de sen^5(x) dx e Trapézio

Assim, de forma bastante simplificada, podemos entender esses métodos como uma maneira de estimar a área sob uma curva calculando a área de trapézios que se ajustam à curva.

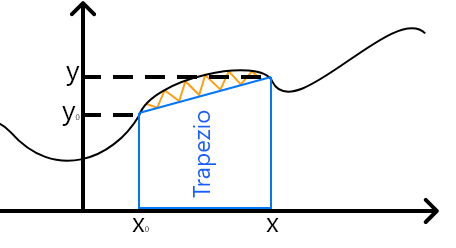
Nesse trapézio a área é (lembra lá da geometria? – Base maior mais base menor vezes altura tudo dividido por dois? ): Então, Base maior é o y, base menor y₀ e a altura h é o x-x₀ .

Assim, a área (integral) seria aproximada por um trapézio. Há de concordar que não precer ser uma boa aproximação certo? Certo, e não é! Mas e se dividir em trapézios ainda menores e somar as áreas? Ai onde está o pulo do gato é exatamente isso que faremos no “trapézio repetido” (nome correto, porém muitas vezes só chamanos de trapézio).

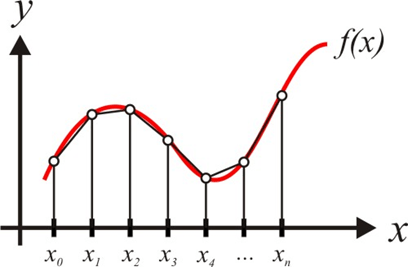
Nesse esquema todo, estamos meio que dividindo a área sob a curva em vários trapézios pequenininhos, certo? E quanto mais trapézios usarmos, mais precisos nossos cálculos se tornarão. O método do trapézio é como uma aproximação “bruta” que fica mais precisa conforme usamos mais e mais trapézios.

Definição formal da Regra de Trapézio Repetido

Primeiramente, a abordagem anterior é uma abordagem prática, mas não podemos deixar de lado a parte mais formal. Assim, a Regra do Trapézio é uma técnica de aproximação da integral de uma função por meio de um polinômio de primeiro grau, ou seja, uma reta. Dessa maneira, para aplicar essa regra, escolhemos dois pontos no intervalo de integração, denotados como (a, f(a)) e (b, f(b)), onde ‘a’ e ‘b’ são os limites do intervalo.

A reta é então definida de tal forma que passe por esses dois pontos, criando um trapézio entre a curva da função e o eixo x no intervalo [a, b]. Por fim, a integral da função nesse intervalo é aproximada pela área desse trapézio.

A fórmula para essa aproximação é a seguinte:

Contudo, essa fórmula considera a média das alturas da função nos pontos ‘a’ e ‘b’ e multiplica pelo comprimento da base do trapézio (b – a). Assim, isso fornece uma estimativa da integral da função no intervalo [a, b] usando uma única área de trapézio. Pois, quanto mais trapézios são usados em uma subdivisão do intervalo, mais precisa será a aproximação da integral. Esse método é comumente utilizado na prática para calcular integrais definidas de funções quando não é possível encontrar uma solução analítica exata.

Na Regra do Trapézio, aproximamos a função f(x) no intervalo [a, b] por uma reta. No entanto, essa aproximação não é exata e há um erro associado a ela. O erro é dado por:

onde:

• ε é o erro na aproximação da integral.
• f”(τ) é a segunda derivada da função f(x) avaliada em um ponto τ no intervalo [a, b], lembrando que não havendo função, dever ser encontrado de forma numérica (o que perde o sentido, mas vai lá, é a teoria).
• h é o comprimento do subintervalo, dado por h = b – a.

O valor de τ está entre ‘a’ e ‘b’, ou seja, a ≤ τ ≤ b.

Essa fórmula nos diz que o erro na Regra do Trapézio é proporcional ao cubo do comprimento do subintervalo (h^3) e à segunda derivada da função no intervalo [a, b]. Quanto menor for o subintervalo (h), menor será o erro, tornando a aproximação da integral mais precisa.

Essa fórmula é útil para estimar o erro e decidir quantos subintervalos devem ser usados para obter uma aproximação suficientemente precisa da integral de uma função quando se aplica a Regra do Trapézio. Quanto menor você deseja que seja o erro, mais subintervalos devem ser usados na subdivisão do intervalo [a, b].

 Integral de sen^5(x) dx e a Regra do Trapézio Composta

Com efeito, a Regra do Trapézio Composta, que é uma maneira de diminuir o erro associado à Regra do Trapézio ao subdividir o intervalo de integração em vários subintervalos e calcular a aproximação da integral para cada subintervalo separadamente.

Na Regra do Trapézio Composta, o intervalo inicial [a, b] é dividido em ‘n’ subintervalos de largura igual, denotada como h. Em seguida, a Regra do Trapézio é aplicada a cada um desses subintervalos separadamente para calcular a aproximação da integral em cada subintervalo.

Dessa maneira, temos que:

com h sendo:

e xi como :

e i o número de intervalos:

Para cada subintervalo ‘i’, a aproximação da integral é calculada da seguinte forma:

Ou seja:

• Com efeito, A_i é a aproximação da integral no subintervalo ‘i’.
• Assim como h é a largura do subintervalo, que é a mesma para todos os subintervalos.
• Sendo assim, f(x_i-1) é o valor da função no ponto inicial do subintervalo ‘i’.
• f(x_i) é o valor da função no ponto final do subintervalo ‘i’.

Com efeito, depois de calcular a aproximação da integral para cada subintervalo usando a Regra do Trapézio, você pode somar todas essas aproximações para obter uma estimativa da integral no intervalo [a, b]. Essa abordagem composta ajuda a reduzir o erro global, uma vez que leva em consideração as variações na função em cada subintervalo. Quanto mais subintervalos você usar (ou seja, quanto menor for ‘h’), mais precisa será a aproximação da integral.

Então.. resolvendo nossa integral

Primeiro vamos definir um intervalo a = 0 e b = 2, e o número de subintervalos n = 6.

Como não temos os dados, vamos primeiro criar os valores de x_i:

h sendo:

e xi como :

então temos (vamos usar 5 casas decimais de aproximação):

Portanto, agora precisamos aplicar esses valores na função (também com 5 casas decimais) :

Enfim, agora, vamos fazer as “multiplicações, para ficar claro, vamos fazer passo a passo:

Assim, encontramos o valor, a nível de curiosidade, o valor real é aproximadamente 0,90393! Dessa maneira, com apenas 6 subintervalos, tivemos uma boa aproximação, lembrando que quanto maior o valor de n, mais próximo do valor real. Nesse sentido, as regras de simpsons, para um mesmo n, serão mais precisas que trapézio.

Integral de sen^5(x) dx e o Algorítmo em Python (Colab)

import math

def trapezio_meuguru(f, a, b, n):
    # Calcula o tamanho do subintervalo
    h = (b - a) / n

    # Inicializa a soma
    integral = 0.0

    # Calcula a integral usando a regra do trapézio
    integral += f(a) / 2.0  # Primeiro termo

    for i in range(1, n):
        x = a + i * h
        integral += f(x)

    integral += f(b) / 2.0  # Último termo

    # Multiplica pela largura do subintervalo
    integral *= h

    return integral

# Função de exemplo (substitua pela sua própria função)
def exemplo_funcao(x):
    return math.sin(x)**5


# Limites de integração
a = 0.0
b = 2.0

# Número de subintervalos
n = 6

# Calcula a integral usando a regra do trapézio
resultado = trapezio_meuguru(exemplo_funcao, a, b, n)
print("Resultado:", resultado)

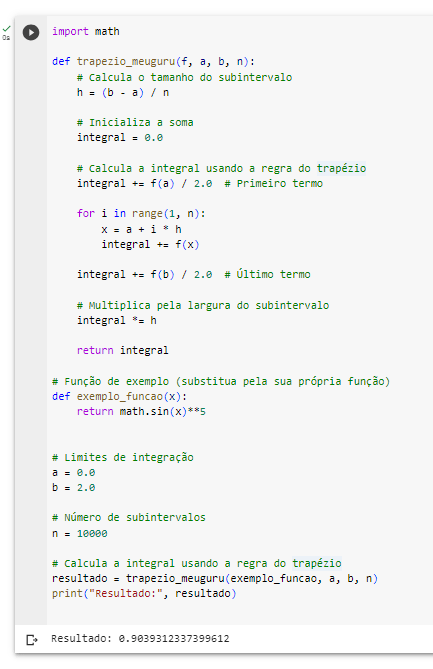
O resultado é 0.8904871160903506 para n = 6, porém, fazendo uma simulação com n = 10000, vimos que o resultado se aproximou do valor real.

Referências sobre a integral de sen^5(x) dx:

Veja Mais: