Integral de sen ^ 5(x) dx – Método numérico 2

Em primeiro lugar, vamos continuar com a nossa amiga, já a resolvemos analíticamente e utilizamos um método numérico de Trapézio, hoje vamos de 1/3 de Simpson. E assim…, não se preocupe, pois exploraremos todos os detalhes dessa técnica, a qual pode ser chamada também de: Integral de sen ^5(x) dx.

De maneira geral, como já vimos o processo de resolução utilizando os métodos numéricos baseia-se em dividir o intervalo em partes iguais, encontrar valores igualmente espaçados dentro dessas partes, multiplicá-los por um “vetor” característico que depende do método escolhido e, em seguida, realizar operações simples de somatório e multiplicação. Abordaremos, então, esses detalhes em breve. Por enquanto, vamos nos aprofundar um pouco mais na parte teórica.

Integral de: sen^5(x) dx e 1/3 de Simpson

Contudo, a regra 1/3 de Simpson é uma técnica de integração numérica que utiliza uma parábola para estimar a função no intervalo de integração. Pois essa abordagem tem uma vantagem significativa sobre a regra do trapézio, pois resulta em um erro de aproximação menor.

Assim, para aplicar a regra 1/3 de Simpson com sucesso, é necessário utilizar um polinômio de segundo grau. Portanto, para isso, precisamos de um total de três pontos que se ajustem à função. Então, dois desses pontos são obtidos nas extremidades do intervalo de integração, sendo o primeiro ponto representado por x₀ = a e o último ponto por x₂ = b.

Assim, o terceiro ponto, x₁, pode ser escolhido em qualquer lugar dentro do intervalo [a, b]. No entanto, por convenção, costuma-se posicionar x₁ no ponto médio do intervalo, ou seja, x₁ = (a + b) / 2.

Portanto, com esses três pontos (x₀, x₁ e x₂), podemos criar uma parábola que se ajusta à função no intervalo de integração. Essa parábola é então usada para calcular a integral aproximada da função.

Com efeito, a regra 1/3 de Simpson é uma ferramenta útil em cálculos de integração numérica, especialmente quando se deseja uma precisão maior do que a oferecida pela regra do trapézio.

Assim, para garantir que tenhamos dois subintervalos de igual tamanho, podemos definir o ponto x₁ como x₀ + h, onde h é o tamanho do subintervalo. Em outras palavras, h é a diferença entre os pontos de extremidade do intervalo.

$h = \dfrac{(b - a)}{2}$ $h = \dfrac{(b - a)}{2}$

Agora, com os três pontos (x₀, x₁ e x₂) à nossa disposição, podemos encontrar o polinômio de segundo grau que passa por esses pontos usando a técnica de Lagrange. Então, a técnica de Lagrange é uma maneira eficaz de encontrar um polinômio que interpola um conjunto de pontos.

Resolvendo a Integral de sen ^ 5(x) dx
O polinômio interpolador de Lagrange é dado por:

$P(x) = f(x_{0}) * L_{0}(x) + f(x_{1}) * L_{1}(x) + f(x_{2}) * L_{2}(x),$ $P(x) = f(x_{0}) * L_{0}(x) + f(x_{1}) * L_{1}(x) + f(x_{2}) * L_{2}(x),$

onde:

f(x₀), f(x₁) e f(x₂) são os valores da função nos pontos correspondentes, e L₀(x), L₁(x) e L₂(x) são os polinômios de Lagrange associados aos pontos x₀, x₁ e x₂, respectivamente.

Os polinômios de Lagrange são dados por:

$L_{0}(x) = \dfrac{(x - x_{1}) * (x - x_{2})} {(x_{0} - x_{1}) * (x_{0} - x_{2})}$ $L_{0}(x) = \dfrac{(x - x_{1}) * (x - x_{2})} {(x_{0} - x_{1}) * (x_{0} - x_{2})}$

$L_{1}(x) = \dfrac{(x - x_{0}) * (x - x_{2})} {(x_{1} - x_{0}) * (x_{1} - x_{2})}$ $L_{1}(x) = \dfrac{(x - x_{0}) * (x - x_{2})} {(x_{1} - x_{0}) * (x_{1} - x_{2})}$

$L_{2}(x) = \dfrac{(x - x_{0}) * (x - x_{1})} {(x_{2} - x_{0}) * (x_{2} - x_{1})}$ $L_{2}(x) = \dfrac{(x - x_{0}) * (x - x_{1})} {(x_{2} - x_{0}) * (x_{2} - x_{1})}$

Primeiramente, usando esses polinômios de Lagrange, podemos construir um polinômio de segundo grau que passa pelos três pontos dados, o que é essencial para aplicar a regra 1/3 de Simpson com sucesso, e para não ter que desenvolver sempre o polinômio de lagrange, podemos usar a forma simplificada, que é obtida após as operações matemáticas necessárias (se estiver com tempo, basta aplicar a distributiva e ir colocando em evidências os termos comuns, faça pelo menos uma vez na mão, acredite, além de dar confiança tu vai entender muito mais):

$\int_{a}^{b} P_{2}= \frac{h}{3}(y_{0}+y4*y_{1}+y_{2})$ $\int_{a}^{b} P_{2}= \frac{h}{3}(y_{0}+y4*y_{1}+y_{2})$

A Regra 1/3 de Simpson é altamente precisa para polinômios de até terceiro grau, resultando em um erro zero. No entanto, para funções de ordem maior (polinômios de grau superior a três) ou funções não polinomiais, o erro não é zero e precisa ser calculado.

Integral de sen ^5(x) dx e o erro na Regra 1/3 de Simpson para funções de ordem superior e como ele pode ser calculado usando a seguinte expressão:

$\varepsilon =-\frac{1}{90}f^{4}(\tau)h^{5}$ $\varepsilon =-\frac{1}{90}f^{4}(\tau)h^{5}$

Dessa maneira, essa expressão fornece uma estimativa do erro na integral calculada pela Regra 1/3 de Simpson.

Portanto, quanto menor o erro desejado, menor deve ser o valor de (b – a) e a quarta derivada da função f(x) deve ser avaliada ou estimada com precisão.

Entretanto, essa capacidade de estimar o erro torna a Regra 1/3 de Simpson uma técnica de integração numérica poderosa e amplamente utilizada para calcular integrais definidas, especialmente quando a precisão é fundamental.

Regra 1/3 de Simpson Composta e a relação com Integral de sen ^ 5(x) dx

Para melhorar a precisão da Regra de Simpson 1/3, você pode subdividir o intervalo [a, b] em 2n subintervalos e aplicar a regra n vezes. Essa abordagem visa reduzir o tamanho dos subintervalos, o que levará a uma melhor estimativa numérica da integral

A cada 2 subintervalos calcula-se a Regra 1/3 de Simpson, assim:

A fórmula para essa aproximação é a seguinte:

$A_{1}= \frac{h}{3}\left ( y_{0}+4y_{1}+y_{2} \right )$ $A_{1}= \frac{h}{3}\left ( y_{0}+4y_{1}+y_{2} \right )$

$A_{2}= \frac{h}{3}\left ( y_{2}+4y_{3}+y_{4} \right )$ $A_{2}= \frac{h}{3}\left ( y_{2}+4y_{3}+y_{4} \right )$

…

$I_{\frac{1}{3}} = \frac{h}{3}\left [ y_{0}+4y_{1}+2y_{2} +4y_{3} ... 2y_{2n-2}+ 4y_{2n-1}+ y_{2n}\right ]$ $I_{\frac{1}{3}} = \frac{h}{3}\left [ y_{0}+4y_{1}+2y_{2} +4y_{3} ... 2y_{2n-2}+ 4y_{2n-1}+ y_{2n}\right ]$

O erro fica sendo assim!

$\varepsilon = - \frac{n}{90} f^{4}(\tau)h^{5}$ $\varepsilon = - \frac{n}{90} f^{4}(\tau)h^{5}$

Portanto temos:

ε é o erro na aproximação da integral.
f^4(τ) é a quarta derivada da função f(x) avaliada em um ponto τ no intervalo [a, b], lembrando que não havendo função, dever ser encontrado de forma numérica (o que perde o sentido, mas vai lá, é a teoria).
h é o comprimento do subintervalo, dado por h = b – a.

O valor de τ está entre ‘a’ e ‘b’, ou seja, a ≤ τ ≤ b.

Dessa maneira, essa fórmula é útil para estimar o erro e decidir quantos subintervalos devem ser usados para obter uma aproximação suficientemente precisa da integral.

Portanto, quanto menor você deseja que seja o erro, mais subintervalos devem ser usados na subdivisão do intervalo [a, b] e para esse método n precisa ser múltiplo de 2 (3 pontos, n =0, n=1 e n=2) .

Com efeito tem-se o seguinte capítulo:

Então.. resolvendo nossa integral

Primeiramente, vamos definir um intervalo a = 0 e b = 2, e o número de subintervalos n = 6.

$\int_{0}^{2} sen^{5}(x) dx$ $\int_{0}^{2} sen^{5}(x) dx$

Como não temos os dados, vamos primeiro criar os valores de x_i:

h sendo:

$h =\frac{2-0}{6} = \frac{1}{3}$ $h =\frac{2-0}{6} = \frac{1}{3}$

e xi como :

$x_{i} = a + h_{i}$ $x_{i} = a + h_{i}$

assim temos (vamos usar 5 casas decimais de aproximação):

$x_{0} = 0$ $x_{0} = 0$

$x_{1} = x_{0} + \frac{1}{3} = 0,33333$ $x_{1} = x_{0} + \frac{1}{3} = 0,33333$

$x_{2} = x_{1} + \frac{1}{3} = 0,66667$ $x_{2} = x_{1} + \frac{1}{3} = 0,66667$

$x_{3} = x_{2} + \frac{1}{3} = 1,00000$ $x_{3} = x_{2} + \frac{1}{3} = 1,00000$

$x_{4} = x_{3} + \frac{1}{3} = 1,33333$ $x_{4} = x_{3} + \frac{1}{3} = 1,33333$

$x_{5} = x_{4} + \frac{1}{3} =1,66667$ $x_{5} = x_{4} + \frac{1}{3} =1,66667$

$\[ x_{6} = x_{5} + \frac{1}{3} = 2,00000\ ] Dessa maneira, agora precisamos aplicar esses valores na função (também com 5 casas decimais) : \[ f(x) =sen^{5}(x)\]” title=”Rendered by QuickLaTeX.com” data-lazy-src=”https://escolaeducacao.org/wp-content/uploads/2024/08/1723729852_846_Integral-de-sen-^-5x-dx-–-Metodo-numerico-2.png”><img loading=$ $f(x_{0}) =sen^{5}(x_{0}) = sen^{5}(0) = 0$ $f(x_{0}) =sen^{5}(x_{0}) = sen^{5}(0) = 0$

$f(x_{1}) =sen^{5}(x_{1}) = sen^{5}(0,33333) = 0,00375$ $f(x_{1}) =sen^{5}(x_{1}) = sen^{5}(0,33333) = 0,00375$

$f(x_{2}) =sen^{5}(x_{2}) = sen^{5}(0,66667) = 0,09042$ $f(x_{2}) =sen^{5}(x_{2}) = sen^{5}(0,66667) = 0,09042$

$f(x_{3}) =sen^{5}(x_{3}) = sen^{5}(1,00000) = 0,42189$ $f(x_{3}) =sen^{5}(x_{3}) = sen^{5}(1,00000) = 0,42189$

$f(x_{4}) =sen^{5}(x_{4}) = sen^{5}(1,33333) = 0,86735$ $f(x_{4}) =sen^{5}(x_{4}) = sen^{5}(1,33333) = 0,86735$

$f(x_{5}) =sen^{5}(x_{5}) = sen^{5}(1,66667) = 0,97725$ $f(x_{5}) =sen^{5}(x_{5}) = sen^{5}(1,66667) = 0,97725$

$f(x_{6}) =sen^{5}(x_{6}) = sen^{5}(2,00000) = 0,62163$ $f(x_{6}) =sen^{5}(x_{6}) = sen^{5}(2,00000) = 0,62163$

Prontinho, assim, agora, vamos fazer as “multiplicações”, para ficar claro, vamos fazer passo a passo:

$A_i = \frac{h}{3}\left [ y_{0}+4y_{1}+2y_{2} +4y_{3} ... 2y_{2n-2}+ 4y_{2n-1}+ y_{2n}\right ]$ $A_i = \frac{h}{3}\left [ y_{0}+4y_{1}+2y_{2} +4y_{3} ... 2y_{2n-2}+ 4y_{2n-1}+ y_{2n}\right ]$

$A_i = (\frac{1/3}{3}) * [f(x_{0}) + 4*f(x_{1}) +2*f(x_{2}) +4*f(x_{3}) + 2*f(x_{4}) + 4*f(x_{5}) + f(x_{6}) ]$ $A_i = (\frac{1/3}{3}) * [f(x_{0}) + 4*f(x_{1}) +2*f(x_{2}) +4*f(x_{3}) + 2*f(x_{4}) + 4*f(x_{5}) + f(x_{6}) ]$

$A_i = (\frac{1}{9}) * [0 + 4*(0,00375) +2*(0,09042)+4*(0,42189) + 2*(0,86735) + 4*(0,97725)+ 0,62163 ]$ $A_i = (\frac{1}{9}) * [0 + 4*(0,00375) +2*(0,09042)+4*(0,42189) + 2*(0,86735) + 4*(0,97725)+ 0,62163 ]$

$A_i = (\frac{1}{9}) * [0 + 0,01500 + 0,18083 + 1,68755 + 1,73469 + 3,90900 + 0,62163 ]$ $A_i = (\frac{1}{9}) * [0 + 0,01500 + 0,18083 + 1,68755 + 1,73469 + 3,90900 + 0,62163 ]$

$A_i = (\frac{1}{9}) * [8,14869]$ $A_i = (\frac{1}{9}) * [8,14869]$

$A_i = 0,90541$ $A_i = 0,90541$

Assim, encontramos o valor, a nível de curiosidade, o valor real é aproximadamente 0,90393! Dessa maneira, com apenas 6 subintervalos, tivemos uma boa aproximação, lembrando que quanto maior o valor de n, mais próximo do valor real.

Integral de sen ^ 5(x) dx :
Portanto, observe o algorítmo em Python (Colab)

import math

def simpson_1_3_meu_guru(f, a, b, n):
    
    if n % 2 != 0:
        raise ValueError("O número de subintervalos (n) deve ser um número par.")

    h = (b - a) / n
    integral = f(a) + f(b)

    for i in range(1, n):
        x = a + i * h
        if i % 2 == 0:
            integral += 2 * f(x)
        else:
            integral += 4 * f(x)

    integral *= h / 3
    return integral

# Exemplo de uso:
def funcao(x):
    return math.sin(x)**5

a = 0
b = 2
n = 6

resultado = simpson_1_3_meu_guru(funcao, a, b, n)
print(f"Aproximação da integral definida: {resultado}")

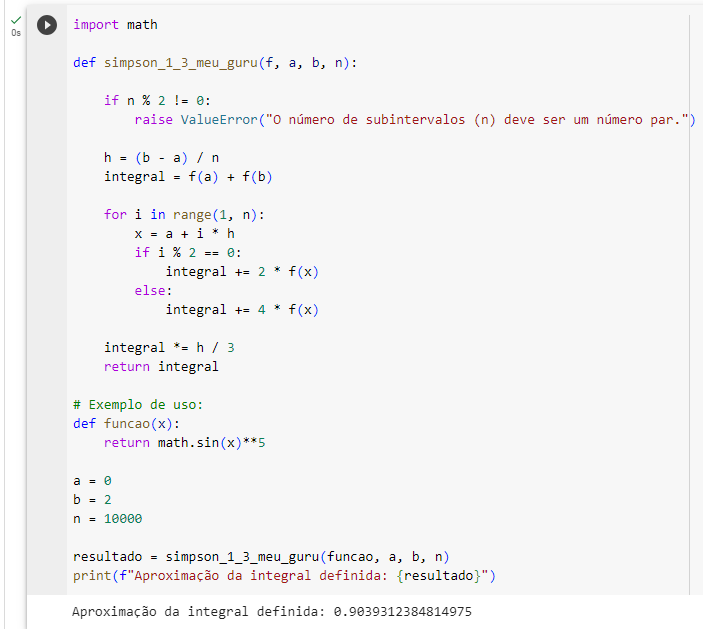
O resultado é 0.9054105856396548 para n = 6, porém, fazendo uma simulação com n = 10000, vimos que o resultado se aproximou do valor real (0.90393).

Referências sobre a Integral de sen ^ 5(x) dx:

Aqui estão as referências que utilizei para lhe explicar sobre o assunto, entretanto é interessante que você sempre olhe o blog, pois traremos novas referências e novidades científicas. Assim, vale muito a pena conhecer outras áreas, bem como dar uma olhada nos demais posts que serão passados no título “veja mais”.

Veja Mais:

Tenho certeza que você quer aprender mais e, por isso deixarei mais glguns posts relacionados à tecnologia, geografia e matemática a fim de que você conheça mais novidades e inove o seu conhecimento sobre tudo !

Ah, não esqueça de nos seguir nas redes sociais, pois, sempre temos uma novidade fresca para você!

What's Hot

The request could not be satisfied

IUCN: As Categorias da Lista Vermelha de Espécies Ameaçadas

Atividades de subtração para imprimir (Ensino Fundamental I)

Integral de sen ^ 5(x) dx – Método numérico 2

The request could not be satisfied

Um tutorial de integrais duplas: Regiões de integração

EDOs: Resolvendo problemas de 1º ordem

Determinantes: Um tutorial prático

Integral de: sen^5(x) dx – Método numérico 3