A álgebra linear é uma das disciplinas introdutórias para todos os cursos das áreas das ciências exatas. Com efeito, essa disciplina urge no contexto da descrição dos sistemas lineares de modo que seja possível realizar o entendimento e solução de problemas que podem ser modelados com noções lineares das variáveis nele contidas.
Entretanto, mesmo sendo uma disciplina extremamente empolgante a álgebra linear é responsável por tirar boas noites de sono dos estudantes frente a sua dificuldade. Com efeito, há vários elementos dessa disciplina que são estritamente teóricos e puros que, por vezes, serão de difícil compreensão e entendimento. Nesse sentido, podemos citar a determinação de autovalores e autovetores de transformações lineares que, por vezes, será assunto de diversas questões das suas listas.
Tendo isso em vista, nesse artigo nós da MeuGuru trazemos a você um tutorial elementar em álgebra linear para o cálculo de autovalores e autovetores. Então, aqui trazemos alguns fundamentos teóricos que embasam essa parte e, por conseguinte, faremos a solução passo a passo de um exercício fundamental dessa disciplina.
Importância e escopo da álgebra linear
Com intuito de amenizarmos um pouco das dores dessa disciplina vamos começar te dando uma motivação ao estudo dessa disciplina. Com efeito, a área da matemática conhecida como álgebra linear é essencial para várias disciplinas acadêmicas e tem aplicações no mundo real. Certamente, ela fornece conceitos e ferramentas poderosos para lidar com sistemas lineares, transformações lineares e espaços vetoriais, por isso é importante.
Assim, a capacidade de resolver sistemas de equações lineares é um componente essencial da álgebra linear. Logo, muitas áreas, como física, engenharia, economia e ciência da computação, usam esses sistemas. Por exemplo, na engenharia, a álgebra linear é usada para análise de circuitos elétricos e resolução de problemas de equilíbrio de forças. Desse modo, ela facilita a compreensão e previsão de fenômenos no mundo real, fornecendo técnicas eficazes para encontrar soluções para esses sistemas complexos.
Além disso, a álgebra linear é fundamental para a modelagem de fenômenos complexos. Com efeito, em campos como economia, ciências ambientais e ciências sociais, é possível descrever e prever comportamentos usando equações lineares e transformações lineares. Ademais, outro campo de atenção é a tomada de decisões informadas, a otimização de processos e a análise de sistemas dinâmicos são todos possibilitados por ele. Nesse sentido a linguagem matemática precisa fornecida pela álgebra linear é usada para representar e resolver problemas que ocorrem no mundo real, o que permite a criação de modelos confiáveis e a obtenção de resultados significativos.
Aplicações físicas da álgebra linear
Certamente, há várias aplicações físicas relevantes dessa área. Em verdade, mesmo os assuntos mais puros como os que tangem aos espaços vetoriais são relevantes em alguns campos da ciência. Em particular, podemos citar a própria teoria quântica ou mecânica quântica a qual baseia-se toda sua formulação na ideia central de espaços vetoriais, mais precisamente os espaços de Hilbert que são espaços vetoriais um tanto quanto mais particulares.
Por outro lado, as noções que perpassam os objetos chamados de Transformações lineares também são fortemente apoiadas nessa área da matemática. Com efeito, nesse escopo as transformações lineares podem significar a descrição da atuação de diversos objetos físicos como ideias de medição de velocidades de partículas, probabilidades de eventos, medições de energia, medições de transporte de calor dentre várias outras características. Logo, esse é um conceito coringa dentro da área o qual por sua vez é fortemente estudado com auxílio de dois outros objetos: autovalores e autovetores.
Autovalores e Autovetores apenas o essencial
Agora, vamos descrever de forma simples e direta o arcabouço teórico que permeia a determinação de autovalores e autovetores. Com efeito, os autovalores e autovetores surgem no contexto de transformações lineares as quais quando em dimensão finita são representadas por matrizes. Então, para fins dos nossos desenvolvimentos consideremos uma matriz A que tenha uma dimensão n, ou seja A é uma matriz quadrada de ordem nxn. Assim, segue que os autovalores de A são os números λ que satisfazem a seguinte igualdade:
det(A – λI) = p(λ) = 0.
Com efeito, veja que os números λ estão multiplicados por I que aqui representa uma matriz quadrada de mesma ordem da matriz A onde os elementos de I são 1 na diagonal principal e 0 em todas as outras posições. Ou seja, a matriz I é a matriz identidade de mesma ordem da matriz A.
O termo p(λ) representa um polinômio em λ chamado de polinômio característico e suas raízes são os autovalores da matriz A.
Agora, podemos já nos ater a determinação dos autovetores. Com efeito, os autovetores são vetores v que são associados ao autovalores λ. Portanto, em geral, para cada autovalor λ há um autovetor v tal que:
(A-λI)v = 0,
onde o termo 0 acima denota o vetor nulo do espaço que estamos trabalhando. Decerto, um autovalor λ pode ter associado mais de um autovetor, entretanto, cada autovetor está associado a um autovalor λ. Logo, de posse desses conhecimentos já é possível determinar-se com exatidão autovalores e autovetores de matrizes/transformações lineares.
Calculando os autovalores com álgebra linear
Para fins de exemplificação vamos calcular os autovalores de uma dada transformação linear T que possua uma matriz A associada que é dada por:
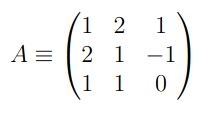
Então, vamos calcular os autovalores λ associados a A. Com efeito, vamos determinar esses números com uso da relação que vimos acima de modo que teremos o seguinte desenvolvimento:
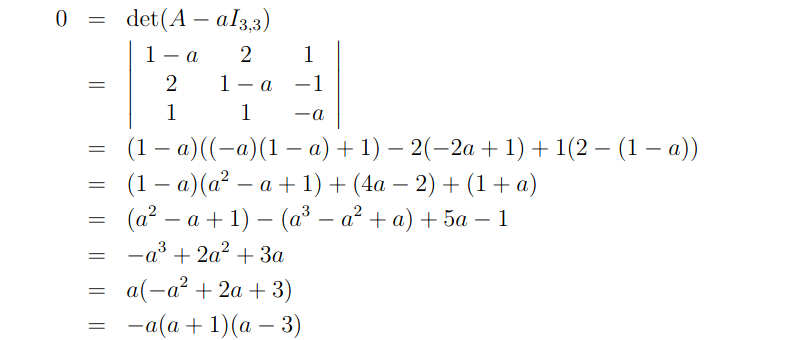
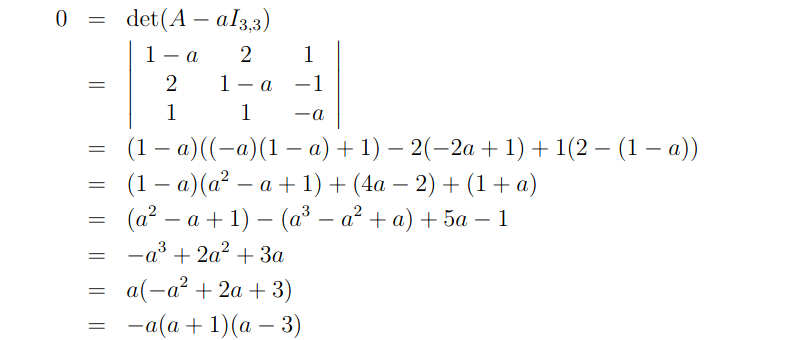
em que I3,3 é chamamos os autovalores de A por a para termos uma correspondência da matriz com os autovalores. Assim, veja que nós temos um polinômio simples onde suas raízes estão quase que explícitas. Portanto, segue que suas raízes são a= 0, a = -1 e a= 3 e esses são os autovalores da matriz.
Calculando os autovetores com álgebra linear
Agora, uma vez que temos os autovalores da matriz podemos então calcular os autovetores associados a cada um dos autovalores anteriores. Então, usando a relação que citamos anteriormente
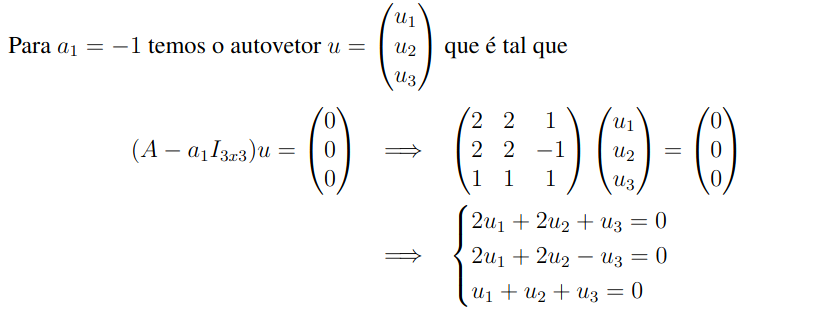

logo, chegamos a um sistema linear simples que resolveremos. Com efeito, veja que se subtrairmos as duas primeiras equações teremos que a terceira componente do autovetor u é nula. Por outro lado, calculando os termos a partir da última equação temos que as componentes tem sinal contrário.
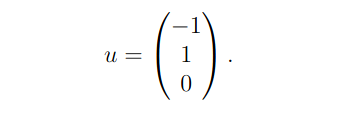
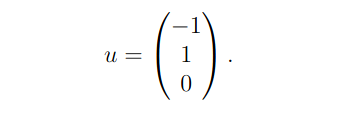
Agora, para o autovalor nulo. Segue o seguinte desenvolvimento que é totalmente análogo:


Veja que a última equação nos revela que as componentes 1 e 2 de v tem sinal contrário. Levando isso em qualquer uma das duas equações acima nós teremos que a última componente deve ter o mesmo sinal que a primeira e logo o autovetor v fica escrito assim
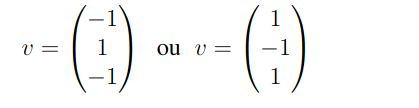
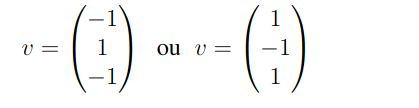
Por fim, resta determinarmos o autovetor associado ao autovalor a =3. Entretanto, esse aqui ficará como exercício para você gurunauta. Certamente, você já deve ser capaz de conseguir fazer isso facilmente uma vez que o processo é essencialmente análogo ao que foi feito anteriormente.
Referências
- STRANG, Gilbert. Álgebra Linear e suas Aplicações. 3ª ed. São Paulo: Cengage Learning, 2014.
- LANG, Serge. Introduction to Linear Algebra. New York: Springer, 2017.
- AXLER, Sheldon. Linear Algebra Done Right. 3rd ed. New York: Springer, 2015.
- MEYER, Carl D. Matrix Analysis and Applied Linear Algebra. Philadelphia: Society for Industrial and Applied Mathematics, 2000.
- KHAN ACADEMY. Khan Academy. Disponível em: < ↗>. Acesso em: 6 set. 2023.
- MIT OPENCOURSEWARE. MIT OpenCourseWare. Disponível em: < ↗>. Acesso em: 6 set. 2023.
- WOLFRAM MATHWORLD. MathWorld. Disponível em: < ↗>. Acesso em: 6 set. 2023.
- BEACHY, John A. Linear Algebra Toolkit. Disponível em: < ↗~beachy/linear_algebra/>. Acesso em: 6 set. 2023.